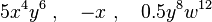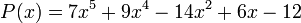monomios

Monomios

Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.

El coeficiente del monomio es el número que aparece multiplicando a las variables.

La parte literal está constituida por las letras y sus exponentes.

El grado de un monomio es la suma de todos los exponentes de las letras o variables.

Dos monomios son semejantes cuando tienen la misma parte literal.Monomio es una expresión algebraica en la que se utilizan exponentes naturales de variables literales que constan de un solo término (si hubiera una suma o una resta sería un binomio), un número llamado coeficiente. Las únicas operaciones que aparecen entre las letras son el producto y la potencia de exponentesnaturales. Se denomina polinomio a la suma de varios monomios. Un monomio es una clase de polinomio con un único término.

Ejemplos:

5x^4y^6 \; , \quad -x \; , \quad 0.5 y^8w^{12}

Son monomios, pero:

x^{-1} \; , \quad 5x^{3/2}

no son monomios, porque los exponentes no son naturales.

polinomios

Polinomios

Un polinomio es una expresión algebraica de la forma:

P(x) = a_nxⁿ+ a_{n - 1}x^{n - 1}+ a_{n - 2}x^{n - 2} + ... + a₁x¹ + a₀

Siendo a_n, a_{n - 1} ... a₁ , a_o números, llamados coeficientes.

n un número natural.

x la variable o indeterminada.

a_o es el término independiente.

Grado de un polinomio

El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x.

Polinomio completo

Es aquel que tiene todos los términos desde el término independiente hasta el término de mayor grado

Polinomio ordenado

Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado.

Un monomio es una expresión algebraica en la que se utilizan letras, números y signos de operaciones. Las únicas operaciones que aparecen entre las letras son el producto y la potencia de exponente natural. Se denomina polinomio a la suma de varios monomios. Un monomio es un polinomio con un único término.

Elementos de un monomio

Un monomio posee una serie de elementos con denominación propia.

Dado el monomio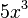 $5x^3 \;$ , se distinguen los siguientes elementos:

coeficiente: $5 \,$
parte literal: $x^3 \,$

El coeficiente de un monomio es el número que aparece multiplicando a la parte literal. Normalmente se coloca al principio. Si tiene valor 1 no se escribe, y nunca puede ser cero ya que la expresión completa tendría valor cero.

Si un monomio carece de coeficiente, este equivale a uno.

Si algún término carece de exponente, este es igual a uno.

Si alguna parte literal no está presente, pero se requiere, entonces se considera con exponente cero, ya que: $\forall x \in \mathbf{R}: x^{0} = 1 \,$

Dada una variable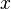 $x \;$ , un número natural 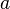$a \;$ y un número real $\alpha \;$ la expresión $\alpha \cdot x^a =\alpha x^a \,$ es un monomio.

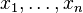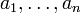Si tenemos varias variables: $x_1,\ldots,x_n$ , el número real $\alpha \;$ y los números naturales $a_1,\ldots,a_n \,$ , el producto correspondiente 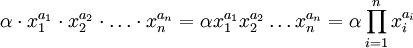$\alpha \cdot x_1^{a_1}\cdot x_2^{a_2}\cdot\ldots \cdot x_n^{a_n} = \alpha x_1^{a_1} x_2^{a_2}\ldots x_n^{a_n} =\alpha \prod_{i=1}^{n}x_{i}^{a_{i}}\,$ también es un monomio.

Grado de un monomio

El grado de un monomio es igual a la suma de los exponentes de las variables que lo componen.

Ejemplos

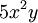$5x^2 y \;$ tiene grado 3

pues equivale a la expresión: 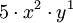$5\cdot x^2 \cdot y^1 \;$ y la suma de los exponentes es 2 + 1 = 3

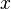$x \;$ tiene grado 1

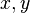pues equivale a $1x^1 \;$ y respecto de $x, y\;$ a la expresión: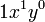 $1x^1 y^0 \;$

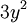$3y^2 \;$ tiene grado 2

y equivale respecto de 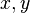$x, y\;$ a la expresión: $1x^0 3y^2 \;$

En matemática se considera que el número cero es un monomio de grado “menos infinito” con el fin de que se respete la regla de que el grado del producto de los monomios es igual a la suma de los grados de los factores.

Polinomio, en matemáticas, se denomina a la suma de variosmonomios, llamados términos del polinomio. Es una expresión algebraica constituida por una o más variables, utilizando solamente operaciones de adición, sustracción, multiplicación yexponentes numéricos positivos. El polinomio de un sólo término se denomina monomio, el de dos binomio, el de tres trinomio.

La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:

$P(x)= a_n x^{n} + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_2 x^2 + a_1 x + a_0 \,$

por ejemplo:

$P(x)= 7 x^5 + 9 x^4 - 14 x^2 + 6 x - 12 \,$

Se denomina grado de un polinomio a la mayor potencia de los monomios que lo componen.

Definición algebraica

Para a₀, …, a_n constantes en algún anillo (en particular podemos tomar un cuerpo, como $\mathbb{R}$ o $\mathbb{C}$ , en cuyo caso los coeficientes del polinomio serán números) con a_ndistinto de cero, para n > 0, entonces un polinomio, P, de grado nen la variable x es un objeto de la forma

$P(x) = a_n x^n + a_{n - 1} x^{n - 1}+ \cdots + a_1 x^{1} + a_0 x^{0}.$

El polinomio se puede escribir más concisamente usandosumatorios como

$P(x) = \sum_{i = 0}^{n} a_{i} x^{i}.$

Las constantes a₀, …, a_n se llaman los coeficientes del polinomio. Aa₀ se le llama el coeficiente constante (o término independiente) y a a_n, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normado. Siendo x un símbolo llamado indeterminada.

https://drive.google.com/open?id=0BwxM60UJCfKrODlvMVk2UXh1alE